Calder Morton-Ferguson

2024

1. 

   Perverse sheaves and t-structures on the thin and thick affine flag varieties

   Roman Bezrukavnikov, and Calder Morton-Ferguson

   Sep 2024

   Abs arXiv

   We study the categories of Iwahori-equivariant perverse sheaves on the thin and thick affine flag varieties associated to a split reductive group G. An earlier work of the first author describes perverse sheaves on the thin flag variety in terms of bimodules over the so-called non-commutative Springer resolution. We partly extend this result to the thick flag variety, providing a similar description for its anti-spherical quotient. The long intertwining functor realizes sheaves on the thick flag variety as the Ringel dual of the category of sheaves on the thick flag variety, we point out that it shares some exactness properties with the similar functor acting on perverse sheaves on the finite-dimensional flag variety. We use this result to resolve a conjecture of Arkhipov and the first author, proving that the image in the Iwahori-Whittaker category of any convolution-exact perverse sheaf on the affine flag variety is tilting.

2. 

   Symplectic Fourier–Deligne Transforms on G/U and the Algebra of Braids and Ties

   Calder Morton-Ferguson

   International Mathematics Research Notices, Apr 2024

   Abs arXiv HTML PDF

   We explicitly identify the algebra generated by symplectic Fourier–Deligne transforms (i.e., convolution with Kazhdan–Laumon sheaves) acting on the Grothendieck group of perverse sheaves on the basic affine space G/U, answering a question originally raised by A. Polishchuk. We show it is isomorphic to a distinguished subalgebra, studied by I. Marin, of the generalized algebra of braids and ties (defined in Type A by F. Aicardi and J. Juyumaya and generalized to all types by Marin), providing a connection between geometric representation theory and an algebra defined in the context of knot theory. Our geometric interpretation of this algebra entails some algebraic consequences: we obtain a short and type-independent geometric proof of the braid relations for Juyumaya’s generators of the Yokonuma–Hecke algebra (previously proved case-by-case in types A, D, E by Juyumaya and separately for types B, C, F4, G2 by Juyumaya and S. S. Kannan), a natural candidate for an analogue of a Kazhdan–Lusztig basis, and finally an explicit formula for the dimension of Marin’s algebra in Type A_n (previously only known for n < 5).

3. 

   Heaps, crystals, and preprojective algebra modules

   Anne Dranowski, Balázs Elek, Joel Kamnitzer, and Calder Morton-Ferguson

   Selecta Mathematica, Oct 2024

   Abs arXiv HTML PDF

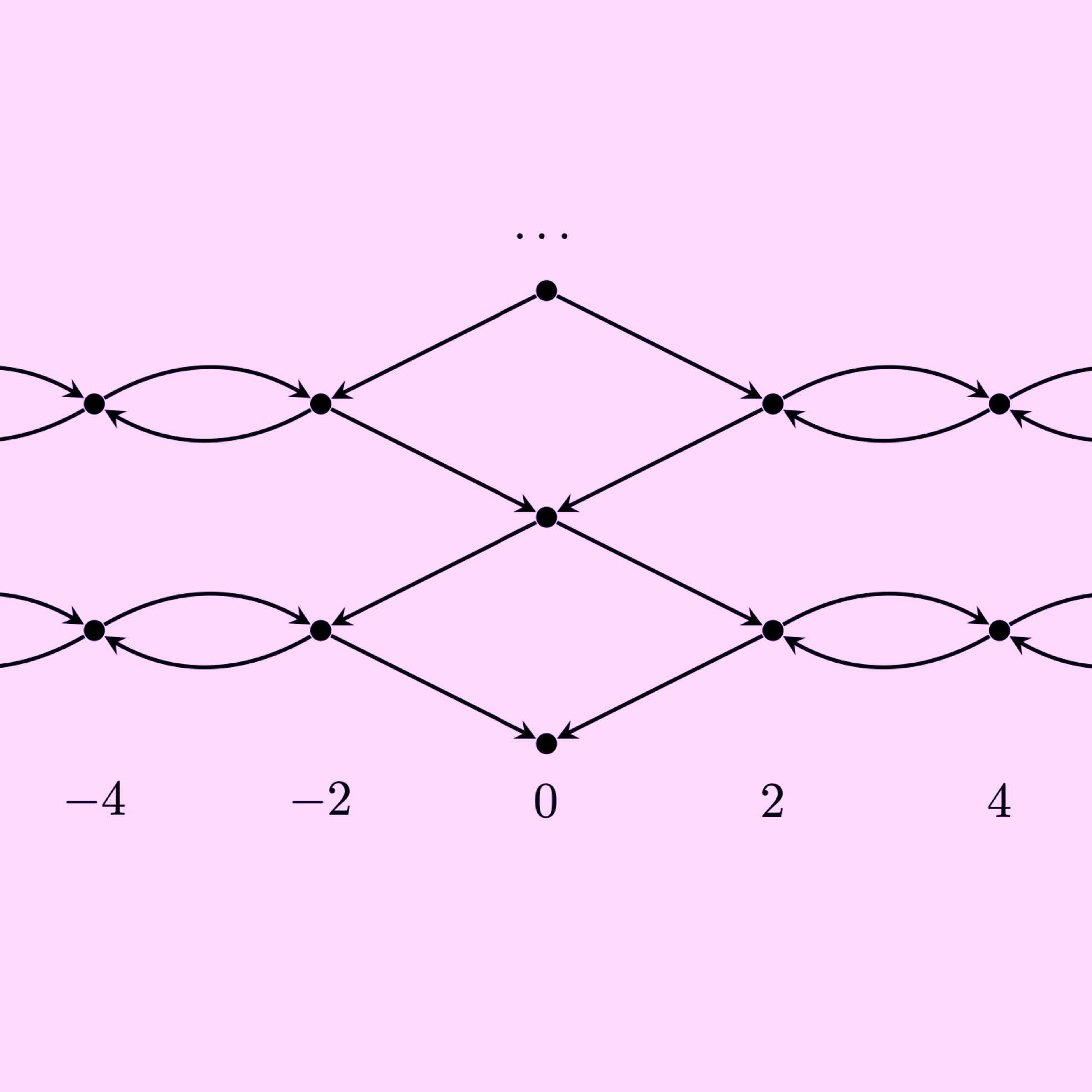
   Fix a simply-laced semisimple Lie algebra. We study the crystal B(nλ), were λ is a dominant minuscule weight and n is a natural number. On one hand, B(nλ) can be realized combinatorially by height n reverse plane partitions on a heap associated to λ. On the other hand, we use this heap to define a module over the preprojective algebra of the underlying Dynkin quiver. Using the work of Saito and Savage-Tingley, we realize B(nλ) via irreducible components of the quiver Grassmannian of n copies of this module. In this paper, we describe an explicit bijection between these two models for B(nλ) and prove that our bijection yields an isomorphism of crystals. Our main geometric tool is Nakajima’s tensor product quiver varieties.

2023

1. 

   Polishchuk’s conjecture and Kazhdan-Laumon representations

   Calder Morton-Ferguson

   Sep 2023

   Abs arXiv

   In their 1988 paper "Gluing of perverse sheaves and discrete series representations," D. Kazhdan and G. Laumon constructed an abelian category A associated to a reductive group G over a finite field with the aim of using it to construct discrete series representations of the finite Chevalley group G(F_q). The well-definedness of their construction depended on their conjecture that this category has finite cohomological dimension. This was disproven by R. Bezrukavnikov and A. Polishchuk in 2001, who found a counterexample in the case G = SL_3. In the same paper, Polishchuk then made an alternative conjecture: though this counterexample shows that the Grothendieck group K_0(A)$ is not spanned by objects of finite projective dimension, he noted that a graded version of K_0(A) can be thought of as a module over Laurent polynomials and conjectured that a certain localization of this module is generated by objects of finite projective dimension, and suggested that this conjecture could lead toward a proof that Kazhdan and Laumon’s construction is well-defined. He proved this conjecture in Types A_1, A_2, A_3, and B_2. In the present paper, we prove Polishchuk’s conjecture in full generality, and go on to prove that Kazhdan and Laumon’s construction is indeed well-defined, giving a new geometric construction of discrete series representations of G(F_q).

2022

1. 

   Kazhdan-Laumon Category O, Braverman-Kazhdan Schwartz space, and the semiinfinite flag variety

   Calder Morton-Ferguson

   Oct 2022

   To appear in Representation Theory, accepted Nov. 2024

   Abs arXiv

   We define and study an analogue of Category O in the context of Kazhdan and Laumon’s gluing construction for perverse sheaves on the basic affine space. We explicitly describe the simple objects in this category, and we show its linearized Grothendieck group is isomorphic to a natural submodule of Lusztig’s periodic Hecke module. We then provide a categorification of these results by showing that the Kazhdan-Laumon Category O is equivalent to a full subcategory of a suitably-defined category of perverse sheaves on the semi-infinite flag variety.

2021

1. 

   Appendix to "The Mirković-Vilonen basis and Duistermaat-Heckman measures"

   Anne Dranowski, Joel Kamnitzer, and Calder Morton-Ferguson

   Acta Math., Oct 2021

   arXiv HTML PDF